试题详情
- 简答题 用二次拉格朗日插值多项式
的值。插值节点和相应的函数值是（0，0），（0.30，0.2955），（0.40，0.3894）。
-
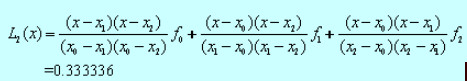
关注下方微信公众号，在线模考后查看
热门试题
- 绘图题：画出SOR迭代法的框图。
- 取步长h=0.2，用预估-校正法解常微分
- 在-4≤x≤4上给出f（x）=e
- 已知下列函数表： （1）写出相应的三次
- 设A为n阶非奇异矩阵且有分解式A=LU，
- 设，则ρ（A）为（）。
- 已知x=φ（x）在区间[a，b]
- 可以生成上述序列。试考察计算Pn的算法的
- 证明：若为严格对角占优矩阵，则A非奇异。
- π=3.14159...具有4位有效数字
- 对矩阵，求||A||&infi
- 设f（x）∈C2
- 插值型求积公式的求积系数之和=（）。其中
- 设x1=1.216
- 为求x3-5x-3
- 已知求解线性方程组Ax=b的分量迭代格式
- 用SOR方法解方程组（分别取松弛因子&o
- 对方程可建立差分公式 试用这一公式求解初
- 证明：当且尽当x和y线性相关x
- 解方程组Ax=b的简单迭代格式x