试题详情
- 简答题 （a）设A是对称阵且a11≠0，经过高斯消去法一步后，A约化为
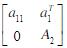证明A2是对称矩阵。 （b）用高斯消去法解对称方程组：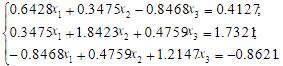 
-
如下：
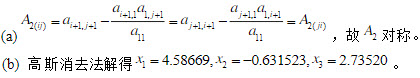
关注下方微信公众号，在线模考后查看
热门试题
- 用n=4的复化梯形公式计算积分，并估计误
- 给定点处的值，试以这3点建立f（x）的2
- 如果，证明用梯形公式计算积分所得到的结果
- 已知数e=2.718281828...，
- 解线性方程组Ax=b的高斯顺序消元法满足
- 用复化梯形公式求积分，问要将积分区间[a
- 设x*是非线性方程
- 用牛顿切线法解方程f（x）=0，选初始值
- 利用尤拉方法计算积分 在点x=0.5，1
- 设A=（aij）&
- 考察下列求积公式具有几次代数精度：
- 比较求ex+10x
- 用辛普森公式求积分并计算误差
- 分别用2.718281，2.718282
- 设A为对称正定矩阵，且其分解为A=LDL
- 数值积分公式的代数精度为（）。
- 取≈1.732计算，下列方法
- 正方形的边长大约为100cm，问怎样测量
- 实数a≠0，考察矩阵，试就方程组A
- 已知函数y=f（x）的相关数据 由牛顿