试题详情
- 简答题 如果
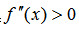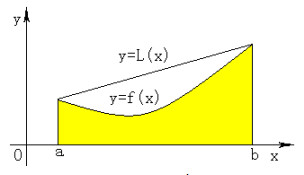
，证明用梯形公式计算积分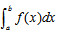
所得到的结果比准确值大，并说明其几何意义。
-
关注下方微信公众号，在线模考后查看
热门试题
- 用Newton法求下列方程的根，计算准
- 用二分法和牛顿法求x-tgx=0的最小正
- 试写出求方程1/x-c=0（其中c为已知
- 计算方法主要研究（）误差和（）误差。
- 设Lk为指标为k的
- 试划出部分选主元素三角分解法框图，并且用
- 用Gauss-Seidel迭代法求解线性
- 利用尤拉公式求解初值问题，其中步长h=0
- 设x1=1.216
- 给定函数f（x），设对一切x，f&pri
- 试讨论用Jacobi迭代法和Gauss-
- 设x的相对误差为2％，求xn<
- 已知求解常微分方程初值问题的数值格式为
- 设A∈Rn×n，求
- 确定下列公式中的待定参数，使其代数精度尽
- 用高斯消去法解方程组
- 取节点x0=0，x
- 写出求解下列方程组的Jacobi迭代格式
- 如有下列表函数： 则一次差商f[0.2
- 写出立方根的牛顿迭代公式（）。