试题详情
- 简答题 设A为对称正定矩阵,且其分解为A=LDLT=WTW,其中W=D1/2LT,求证:
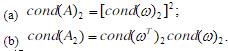
-
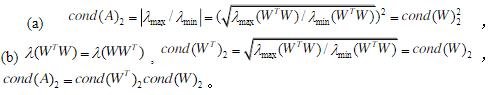
关注下方微信公众号,在线模考后查看

热门试题
- 用梯形方法解初值问题 证明其近似解为
- 数值积分公式是否为插值型求积公式,为什么
- 利用矩阵的LU分解法解方程组
- 设f(x)=x4+
- x*为精确值x的
- 解线性方程组Ax=b的高斯顺序消元法满足
- 利用公式求下列各近似值的误差限: 其中
- 设A为非奇异矩阵,求证
- 设矩阵分解为A=LU,则U=()
- 证明解y′=f(x,y)的下
- 方程x3-x
- 可以生成上述序列。试问计算的上述公式是稳
- 试分别用Jacobi迭代法和Gauss-
- 给定方程x2-x-
- 试用消元法解方程组假定只用三位数计算,问
- 设A=(aij)&
- 3.142和3.141分别作为π的近似数
- 下述矩阵能否分解为LU(其中L为单位下三
- 已知,则A的谱半径ρ(A)=()
- 设求A的LU分解。