试题详情
- 简答题 证明解y′=f（x，y）的下列差分公式
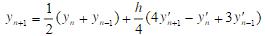是二阶的，并求出截断误差的首项。
-
如下：
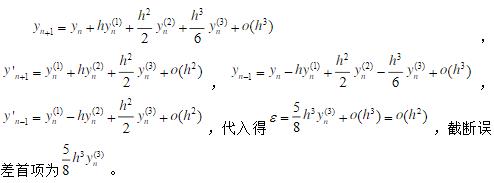
关注下方微信公众号，在线模考后查看
热门试题
- 导出如下3个求积公式，并给出截断误差的表
- f（1）=-1，f（2）=2，f（3）=
- 设x=020013753为真值xr=0.
- 试分别用Jacobi迭代法和Gauss-
- 已知常微分方程的初值问题： 用改进的Eu
- 是第二类切比雪夫多项式，证明它有递推关系
- 设f（x）=（x3
- 用n=4的复化梯形公式计算积分，并估计误
- 用高斯－塞德尔方法解Ax=b，用x
- 试就下列函数讨论牛顿法的收敛性和收敛速度
- 设 计算A的条件数。cound（A）<
- 用简单迭代格式求方程x3
- 确定求积公式中的待定参数，使其代数精确度
- 设x的相对误差为2％，求xn<
- 数值积分公式的代数精度为（）。
- 已知一元方程x3
- 用Gauss-Seidel迭代法求解线性
- 用改进的平方根法解方程组
- 试用Gauss消去法解下列方程组，计算过
- 用龙贝格方法计算积分，要求误差不超过10