试题详情
- 简答题用简单迭代格式求方程x3-x-0.2=0的所有实根,精确至有3位有效数。
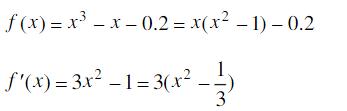




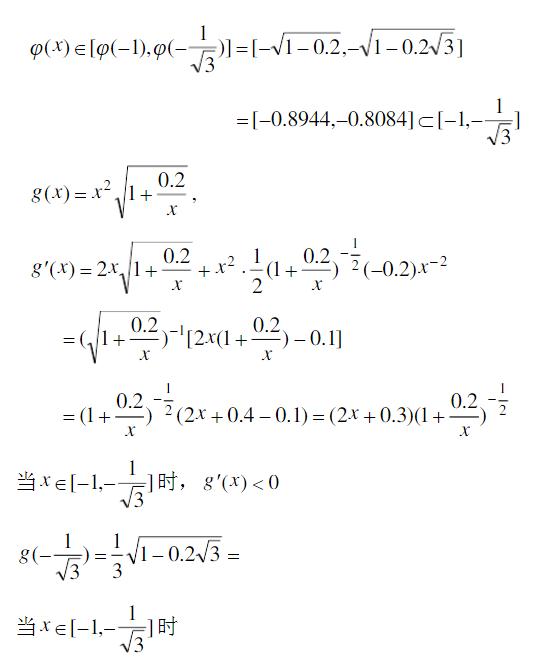

关注下方微信公众号,在线模考后查看

热门试题
- 对于给定的线性方程组 (1)讨论雅可比迭
- 编出用正交多项式做最小二乘拟合的程序框图
- 导出具有下列形式的3阶方法:
- 证明对称矩阵 用雅可比迭代法求解方程组A
- 证明:梯形公式 无条件稳定。
- 证明:(a)如果A是对称正定阵,则A
- 求a,b使为最小。
- 用许瓦兹不等式估计的上界,并用积分中值定
- 已知求解线性方程组Ax=b的分量迭代格式
- 有常微分方程的初值问题,试用泰勒展开法,
- 给出f(x)=lnx的数值表用线性插值及
- 插值型求积公式的求积系数之和()。
- 设方程组 试考察解此方程组的雅可比迭代
- 设f(x)=(x-x0
- 用二分法和牛顿法求x-tgx=0的最小正
- 求证的充要条件是对任何向量x,都有
- 用Gauss-Seidel迭代法解方程组
- 试用初等反射阵A分解为QR,其中Q为正交
- 什么是求积公式的代数精确度?如何利用代数
- 有一圆柱,高为25.00cm,半径为20