试题详情
- 简答题
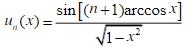是第二类切比雪夫多项式，证明它有递推关系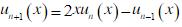
-
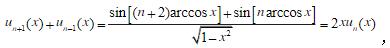
和差化积得证。 关注下方微信公众号，在线模考后查看
热门试题
- 设Ax=b，其中A对称正定，问解此方程组
- 已知一组试验数据如下： 求它的拟合曲线
- 可以生成上述序列。试考察计算Pn的算法的
- 如果方阵A有aij
- 现给出一张记录{xk
- 用梯形方法解初值问题 证明其近似解为
- 数值积分公式的代数精度为（）。
- 若f（x）=a0+
- 用牛顿（切线）法求的近似值。取x
- 若误差限为0.5×10-15<
- 3.142和3.141分别作为π的近似数
- 用梯形法解初值问题y′=x2<
- 用雅可比方法计算 的全部特征值及特征向
- 构造代数精度最高的如下形式的求积公式，并
- f（x）是[-a，a]上的连续奇（偶）函
- 对方程可建立差分公式 试用这一公式求解初
- 把f（x）=arccosx在[-1，1]
- 用二分法求方程x2
- 证明：若为严格对角占优矩阵，则A非奇异。
- 有常微分方程的初值问题，试用泰勒展开法，