试题详情
- 简答题 用高斯-塞德尔方法解Ax=b,用xi(k+1)记x(k+1)的第i个分量,且
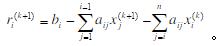 (a)证明
(a)证明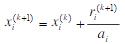 ; (b)如果ε(k)=x(k)-x*,其中x*是方程组的精确解,求证
; (b)如果ε(k)=x(k)-x*,其中x*是方程组的精确解,求证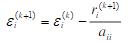 : 其中
: 其中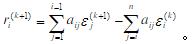 。
。
-
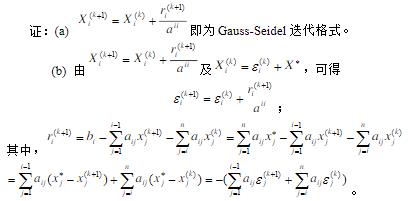
关注下方微信公众号,在线模考后查看

热门试题
- 把f(x)=arccosx在[-1,1]
- 用梯形方法解初值问题 证明其近似解为
- 设 已知方程组Ax=b的精确解为 (1)
- 用二步法求解一阶常微分方程初值问题,问:
- 已知函数值f(0)=6,f(1)=10,
- 用欧拉方法求在点x=0.5,1.0,1.
- 试改变下列表达式,使计算结果比较精确:
- 设A为n阶矩阵,如果称A为对角优势阵。证
- 若则矩阵A的谱半径ρ(A)=()
- 解初始值问题近似解的梯形公式是y
- 已知用线性插值求的近似值。(拉格朗日线性
- 为求方程x3―x<
- 插值型求积公式的求积系数之和()。
- 利用矩阵的LU分解法解方程组
- 设方程组 迭代公式为
- 设求A的LU分解。
- 则=(),=(),=(),=()。
- 给出cos x,0°≦x≦90°的函数表
- 直接验证柯特斯公式具有5次代数精度。
- 下列各数都是经过四舍五入得到的近似数,即