试题详情
- 简答题 设x∈Rn,证明
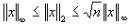 。
。
-
如下:

关注下方微信公众号,在线模考后查看

热门试题
- 设,则A的奇异值为()
- 导出具有下列形式的三阶方法:
- 证明:(a)如果A是对称正定阵,则A
- 构造一个三次多项式H(x),使它满足条件
- 则=(),=(),=(),=()。
- 用改进的尤拉方法解 取步长h=0.1计
- 递推公式,如果取y0
- 设一阶差商f(x1
- 利用初等反射阵将 正交相似约化为对称三
- 设M3=Span{
- 证明:切比雪夫多项式序列
- 求满足下列条件的埃尔米特插值多项式:
- 设初值问题y′=x
- f(x)是[-a,a]上的连续奇(偶)函
- 设A为对称正定矩阵,且其分解为A=LDL
- 数值积分公式是否为插值型求积公式,为什么
- 求证的充要条件是对任何向量x,都有
- 用二分法求方程x3
- 用最小二乘原理求一个形如y=a+bx
- 等距二点求导公式f′(x1)≈()