试题详情
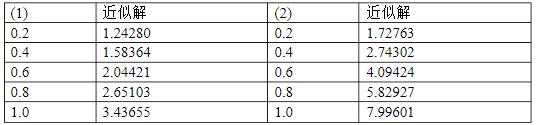
- 简答题 取h=0.2,用四阶经典的龙格-库塔方法求解下列初值问题:

-
如下:
关注下方微信公众号,在线模考后查看

热门试题
- 对矩阵,求||A||&infi
- 设Ax=b,其中A对称正定,问解此方程组
- 求a,b使为最小。
- 求利用梯形公式的计算结果为(),利用辛卜
- 设M3=Span{
- 用辛浦生公式计算积分近似值;
- 设矩阵分解为A=LU,则U=()
- 给定方程f(x)=0,并设x*
- 写出求解方程组的Gauss-Seidel
- 求解初值问题:
- 用高斯-塞德尔方法解Ax=b,用x
- 确定求积公式中的待定参数,使其代数精确度
- 用雅可比、高斯-塞德尔迭代法,求解方程组
- 设已知一组实验数据
- 考察下列求积公式具有几次代数精度:
- 数值求积公式是否为插值型求积公式?为什么
- 试建立一种收敛的Seidel迭代公式,说
- 设f(x)=x7+
- 用LU分解法求解线性方程组
- 利用尤拉方法计算积分 在点x=0.5,1