试题详情
- 简答题 证明矩阵
对于
是正定的，而雅可比迭代只对
是收敛的。
-
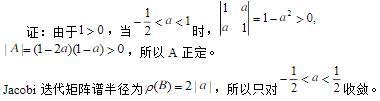
关注下方微信公众号，在线模考后查看
热门试题
- 设Ux=d，其中U为三角矩阵。 （a）
- 用Romberg方法求，要求误差不超过。
- 在[a，b]上求插值多项式H3
- 用最小二乘法求一个形如y=a+bx
- 试确定常数A，B，C和a，使得数值积分公
- 设f（x）=x7+
- 设detA≠0，用a，b表示解方程
- 设求A的LU分解。
- 证明对称矩阵 用雅可比迭代法求解方程组A
- 设一阶差商f（x1
- 在-4≤x≤4上给出f（x）=e
- 设xi（i=0，1
- 用二分法求方程f（x）=x3<
- 分别用二阶显式亚当姆斯方法和二阶隐式亚当
- 对f（x）=sinx在[0，π/2]上求
- 梯形公式具有1次代数精度，Simpson
- 给定规格化的浮点数系F://β=2，n=
- 设f（x）=（x3
- -324.7500是舍入得到的近似值，它
- 用LU分解法求解线性方程组