试题详情
- 简答题证明n阶均差有下列性质:若F(x)=cf(x),则F[x0,x1,...,xn]=cf(x0,x1,...,xn)。
-
如下:
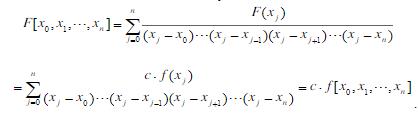
关注下方微信公众号,在线模考后查看

热门试题
- f(x)是[-a,a]上的连续奇(偶)函
- 可以生成上述序列。试问计算的上述公式是稳
- 证明对任意参数t,下列龙格-库塔公式是二
- 求a,b使为最小。
- 写出求解方程组的Gauss-Seidel
- 已知数e=2.718281828...,
- 用二分法求方程x3
- 用直接三角分解(Doolittle)法解
- 给定求积公式试确定a,b,c使它的代数精
- 设有函数值表:
- 设f(x)∈C2
- 若x1≈0.937具有3位有
- 已知一组试验数据如下: 求它的拟合曲线
- 确定下列求积公式中的待定参数,使其代数精
- 通过点(x0,y<
- 设,则A的奇异值为()
- 用1+x近似表示ex
- 设A∈Rn*n,证
- 则=(),=(),=(),=()。
- 计算方法主要研究()误差和()误差。