试题详情
- 简答题 矩阵第一行乘以一数，成为
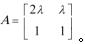证明当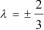
时，cound（A）∞有最小值。
-
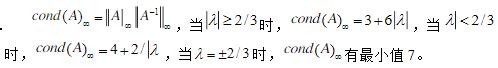
关注下方微信公众号，在线模考后查看
热门试题
- 求f（x）=x2在
- 设fˊ（-1）=1，fˊ（0）=3，fˊ
- 用龙贝格方法计算积分，要求误差不超过10
- 利用积分计算ln4时，若采用复化梯形公式
- 试改变下列表达式，使计算结果比较精确：
- 用列主元消去法解线性方程组
- 用高斯消去法解方程组
- 由高斯消去法说明当Δi
- 若则矩阵A的谱半径ρ（A）=（）
- 试建立一种收敛的Seidel迭代公式，说
- 试分别用Jacobi迭代法和Gauss-
- 试用消元法解方程组假定只用三位数计算，问
- 方阵T分块形式为 其中Tii
- 给定函数f（x），设对一切x，f&pri
- 设 计算A的条件数。cound（A）<
- 取节点x0=0，x
- 研究求的牛顿公式 证明对一切k=1.2
- 用梯形方法解初值问题 证明其近似解为
- （a）设A是对称阵且a11
- 已知： 请依据上述数据求f（x）的2次