试题详情
- 简答题设A∈Rn×n,且ai1,aj1不全为零,Pij为使aj1(2)=0的平面旋转阵,试推导计算PijA第i行,第j行元素公式及APTij第i列,第j列元素的计算公式。
-
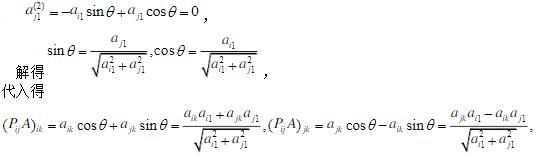
关注下方微信公众号,在线模考后查看

热门试题
- 用雅可比方法计算 的全部特征值及特征向
- 给定线性方程组 (1)写出SOR迭代格
- 观测物体的直线运动,得出以下数据:
- 数值微分中,已知等距节点的函数值(x<
- 设,试说明A为可约矩阵。
- 设f(x)=C2[
- 已知求解线性方程组Ax=b的分量迭代格式
- 证明对于任意选择的A,序列收敛于零
- 用许瓦兹不等式估计的上界,并用积分中值定
- 求证的充要条件是对任何向量x,都有
- 证明对任意参数t,下列龙格-库塔公式是二
- 构造代数精度最高的如下形式的求积公式,并
- 证明:(a)如果A是对称正定阵,则A
- Jacobi迭代法解方程组Ax=b的必要
- 已知,用抛物线插值计算的值并估计截断误差
- x=(3,0,-4,12)T<
- 取5个等距节点 ,分别用复化梯
- 设f(x)=(x3-a)2<
- 试建立一种收敛的Seidel迭代公式,说
- 设A为n阶非奇异矩阵且有分解式A=LU,