试题详情
- 简答题证明晶体宏观对称性中的纯转动只可能有C1,C2,C3,C4,C6五种对称元素。
-
证明:
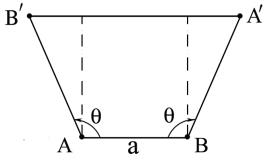
考虑晶格中一格点A,并在A格点最近邻的格点中选一点,记为B,如图所示。让一个旋转轴通过格点A,并且垂直于该晶格面。如果B格点绕A旋逆时针旋转θ角,B点将转到B′位置。因为晶格具有周期性,A和B完全等价。如果转轴通过B点,在B点看来,A点应顺时针旋转,这将使得A格点旋转θ角,到达A′点。
如果旋转θ角是该晶格的一个对称操作,旋转后的B′格点将与没有旋转时的原来点阵中某个格点重合,同样A′格点也将与原来点阵中某个格点分别重合。由图可以发现A′B′平行于AB,同时考虑到B为A的最近邻格点,因此A′B′的长度必然是AB长度的整数倍。设AB两近邻格点的距离为a。
则有

如果有一个对称轴,晶体绕该轴旋转2π/n,后能够和自己重合,我们就成该对称轴为n重轴,这种操作的对称元素通常记为n,简称对称素。从以上证明可以发现,具有周期性即满足的Rl=l1al+l2a2+l3a3的布拉菲格子,其旋转轴必须是C1,C2,C3,C4,C6这五种对称轴,不存在五重轴、七重轴。 关注下方微信公众号,在线模考后查看

热门试题