试题详情
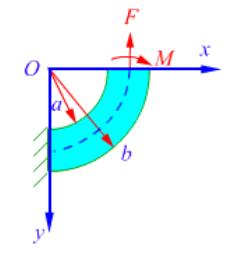
- 简答题 矩形横截面的曲梁,一端固定,自由端处承受集中力F和力矩M的作用,如图所示。设应力函数φf(ρ,φ)= f (ρ)cosφ可以求解该问题,试求出M与F之间的关系,并求曲梁应力。
-

关注下方微信公众号,在线模考后查看

热门试题
- 已知如图所示悬挂板,在O点固定,若板的厚
- 图示悬臂梁,长为l,高为h,l〉〉h,在
- 弹性力学
- 位移法求解的条件是什么?怎样判断一组位移
- 试简述力学中的圣维南原理,并说明它在弹性
- 按应力求解平面问题时常采用()和()。
- 半无限弹性体表面作用集中力F,试用应力函
- 边界条件表示在边界上()与(),或()与
- 矩形截面的柱体受到顶部的集中力和力矩M的
- 一长方形薄板如图所示。其两端受均匀拉伸P
- 已知受力物体内某一点的应力分量为:,试求
- 所谓“完全弹性体”是指()。
- 弹性力学中应力如何表示?正负如何规定?
- 下列关于应力解法的说法正确的是()。
- 试画出下图中矩形薄板的正的体力、面力和应
- 有限元法的基本思想是什么?
- 圣维南原理
- 一组可能的应力分量应满足:(),()。
- 试写出平面问题的应变分量存在的必要条件,
- 楔形体在两侧面上受有均布剪力q,如图,试