试题详情
简答题甲乙两袋各将一只白球一只黑球，从两袋中各取出一球相交换放入另一袋中，这样进行了若干次。以pn，qn，rn分别记在第n次交换后甲袋中将包含两只白球，一只白球一只黑球，两只黑球的概率。试导出pn+1，qn+1，rn+1用pn，qn，rn表出的关系式，利用它们求pn+1，qn+1，rn+1，并讨论当n→∞时的情况。
  • 令Ai，Bi，Ci分别表示第i次交换后，甲袋中有两只白球，一白一黑，两黑球的事件，则由全概率公式得

    初始条件是甲袋一白一黑，乙袋一白一黑，即p0=r0=0，q0=1，由递推关系式得

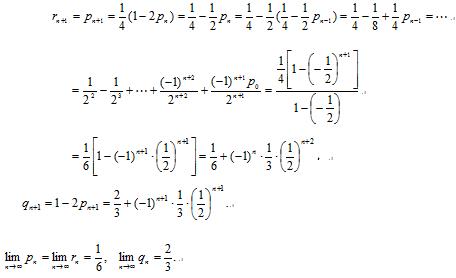
  • 关注下方微信公众号，在线模考后查看

热门试题