试题详情
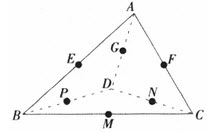
简答题 四面体的顶点和各棱的中点共10个点。 （1）设一个顶点为A，从其他9点中取3个点，使它们和点A在同一平面上，不同的取法有多少种？ （2）在这10点中取4个不共面的点，不同的取法有多少种？
  • （1）如图，含顶点A的四面体的三个面上，除点A外都有5个点，从中取出3点必与点A共面，共有3C53种取法。
    含顶点A的棱有三条，每条棱上有3个点，它们与所对棱的中点共面，共有3种取法，根据分类计数原理和点A共面三点取法共有3C53+3=33种。
    （2）取出的4点不共面比取出的4点共面的情形要复杂，故采用间接法：先不加限制任取4点（C104种取法）减去4点共面的取法。
    取出的4点共面有三类：第一类：从四面体的同一个面上的6点取出4点共面，有4C64种取法；第二类：每条棱上的3个点与所对棱的中点共面，有6种取法；第三类：从6条棱的中点取4个点共面，有3种取法，根据分类计数原理4点共面取法共有4C64+6+3=69。
    故取4个点不共面的不同取法有C104-4C64+6+3）=141（（种）。

  • 关注下方微信公众号，在线模考后查看

热门试题