试题详情
简答题现有线性规划问题 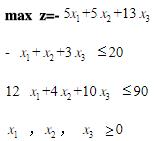先用单纯形法求出最优解，然后分析在下列各种条件下，最优解分别有什么变化？  （1）约束条件1的右端常数20变为30； （2）约束条件2的右端常数90变为70； （3）目标函数中x3的系数变为8； （4）x1的系数向量变为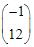； （5）增加一个约束条件2x1+3x2+5x3≤50； （6）将约束条件2变为10x1+5x2+10x3≤100。
  • 把原问题化成标准型的：

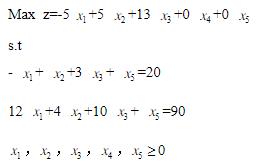
    单纯形法解得,最优解：
    X=（0，20，0，0，10）T
    目标函数最优值为100。
    非基变量x1的检验数等于0，原线性问题有无穷多最优解。
    （1）约束条件1的右端常数变为30
    有Δbˊ=B-1Δb
    因此bˊ=b+Δbˊ
    单纯形法解得，最优解：
    X=（0，0，9，3，0）T
    目标函数最优值为117。
    （2）约束条件2的右端常数变为70
    有Δbˊ=B-1Δb
    因此bˊ=b+Δbˊ
    单纯形法解得，最优解：
    X=（0，0，5，0，0）T
    目标函数最优值为90。
    （3）x3的系数变成8，x3是非基变量，检验数小于0，所以最优解不变。
    （4）x1的系数向量变为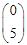
    X1是非基变量，检验数等于-5，所以最优解不变。
    （5）加入约束条件3用对偶单纯形表计算得：
    X=（0，25/2，5/2，0，15，0）T
    目标函数最优值为95。
    （6）改变约束条件P3，P4，P5没有变化，
    线性规划问题的最优解不变。

  • 关注下方微信公众号，在线模考后查看

热门试题