试题详情
简答题 设d维晶体，采用德拜模型，设格波角频率与波矢之间的关系为ω=cq，c为格波在晶格中传输的速度。 （1）证明，d为晶格的声子态密度正比于ωd−1。 （2）证明，低温下d维简谐晶体的比热按Td变化。
  • （1）d维空间的态密度为可表述为：

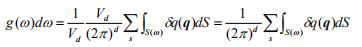
    积分对d维空间中的等能面进行，δq（q）表示等能面上厚度为δq（q）的壳层，由于ω=cq。d维空间，面积元dS与立体角dΩ关系为，dS=qd−1dΩ，得到

  • 关注下方微信公众号，在线模考后查看

热门试题