试题详情
- 简答题 设方程组
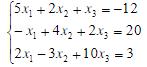（a）考察用雅可比迭代法，高斯-塞德尔迭代法解此方程组的收敛性； （b）用雅可比迭代法，高斯-塞德尔迭代法解此方程组，要求当
时迭代终止。
-
关注下方微信公众号，在线模考后查看
热门试题
- 计算方法实际计算时，对数据只能取有限位表
- 用改进的尤拉方法解初值问题 取步长h=
- 数值微分中，已知等距节点的函数值（x<
- 若线性代数方程组AX=b的系数矩阵A为严
- 用1+x近似表示ex
- 求f（x）=ex在
- 设空间φ1=spa
- 构造代数精度最高的如下形式的求积公式，并
- 确定求积公式中的待定参数，使其代数精确度
- 编出改进FFT算法的程序框图。
- 已知x=[0，-1，2]T
- 在-4≤x≤4上给出f（x）=e
- 设f（x）=（x3
- 有下列数表： 所确定的插值多项式的次数
- 用追赶法解三对角方程组Ax=b，其中
- 设x=020013753为真值xr=0.
- 方程x3-x
- 应用牛顿法于方程x2
- （a）设A是对称阵且a11
- 设 计算A的条件数。cound（A）<