试题详情
简答题袋中有a只黑球，b只白球，甲乙丙三人依次从袋中取出一球（取后不放回），试分别求出三人各自取得白球的概率（b≥3）。
  • A={甲取出一球为白球}，B={甲取出一球后，乙取出一球为白球}，C={甲，乙各取出一球后，丙取出一球为白球}。则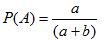，甲取出的球可为白球或黑球，利用全概率公式得

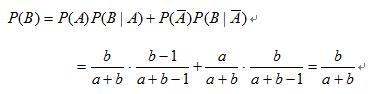
    甲，乙取球的情况共有四种，由全概率公式得

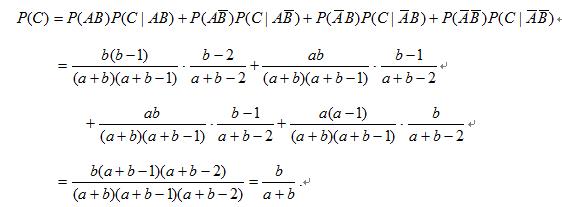
  • 关注下方微信公众号，在线模考后查看

热门试题