试题详情
- 简答题
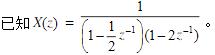 (1)确定与X(z)有关的收敛域可能有几种情况,画出各自的收敛域图; (2)求以上各种收敛域所对应的离散时间序列的表达式; (3)以上序列中哪一种序列存在傅氏变换?
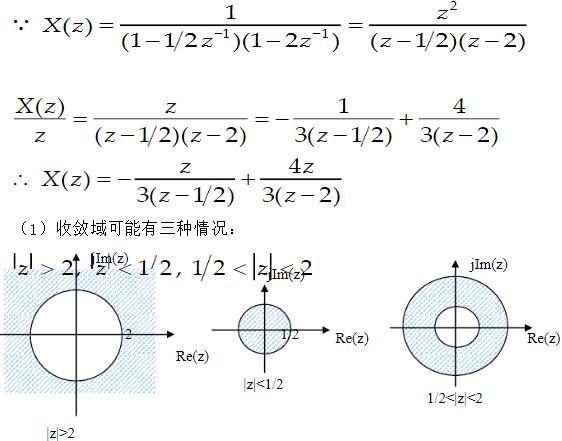
(1)确定与X(z)有关的收敛域可能有几种情况,画出各自的收敛域图; (2)求以上各种收敛域所对应的离散时间序列的表达式; (3)以上序列中哪一种序列存在傅氏变换?
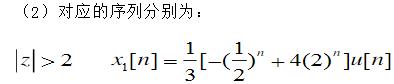

关注下方微信公众号,在线模考后查看

热门试题
- 已知,收敛域Re(s)>0,试求其拉氏反
- 已知信号f(t)的频带宽度为&Delta
- 画出差分方程的结构图。
- 频谱函数F(jω)=2u(1-ω)的傅里
- 信号采样中作DFT、FFT变换,频率分辨
- 建立如图所示各系统的差分方程,并求单位样
- 零状态响应是指系统没有激励时的响应
- 对时间区域(-∞<t<∞)而言,两个时间
- 电路如图所示,已知E=4V,当t<0时,
- 一线性时不变离散时间因果系统的直接型模拟
- 设:两信号f1(t
- 单位样值响应h(n)的Z变换就是系统函数
- 任何信号都可以分解为偶分量与奇分量之和。
- 已知系统微分方程相应的齐次方程为 两系
- 线性性质包含两个内容:()
- 已知系统的微分方程为: 求系统函数H(
- ,属于其零点的是()
- 若Z变换的收敛域是|z|>Rx
- 根据网络函数的极点定性描述其时域单位冲击
- f(t)=2δ(t)-3e-7