试题详情
简答题F公司拟投产一个新产品，预计需要投资1000万元，每年将持续获得现金流105万元，项目的资本成本为10%，无风险利率为5%。 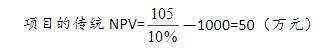以传统NPV方法得出的结论是项目净现值为正，值得投资。但新产品的前景还不明确，是应该立即投资还是先等待观望呢？这就需要衡量隐含的时机选择期权的价值。每年的现金流是平均的预期，并不确定。如果新产品受顾客欢迎，预计现金流量为131.25万元；如果不受欢迎，预计现金流量为84万元。未来现金流量存在不确定性，我们选择二叉树的方法来计算时机选择期权的价值。
  • 1. 构造现金流量和项目二叉树。具体情况见表21-4。

    上行项目价值=131.25/10% =1312.5（万元） 下行项目价值=84/10% = 840（万元）
    2. 期权价值二叉树。
    （1）确定1年末的期权价值。期权的执行价格是投资成本1000万元。
    现金流量上行时期权的价值= 1312.5—1000=321.5（万元）
    现金流量下行时，项目价值为840万元，低于执行价格1000万元，因此期权被放弃，期权价值为0。
    （2）根据风险中性原理计算上行概率，即
    报酬率 =（本年现金流量+期末价值）/年初投资—1 上行报酬率 =（131.25+1312.5）/1000—1=44.38% 下行报酬率 =（84+840）/1000—1= —7.6%
    无风险收益率 = 上行概率*44.38%+（1—上行概率）*（—7.6%）= 5% 求得
    上行概率 = 0.2424 （3） 计算期权价值，即
    期权到期日价值 = 0.2424*312.5+（1—0.2424）*0=75.75（万元） 期权的现值 = 75.75/1.05=72.14（万元）
    3. 判断是否应该延迟投资。如果立刻进行该项目，可以得到净现值50万元，相当于立即执行期权；如果等待，期权的价值为72.14万元，大于立即执行的收益。也就是说，等待失去50万元，但却持有了价值为72.14万元的选择权，因此应当等待。

  • 关注下方微信公众号，在线模考后查看

热门试题