试题详情
- 简答题连续系统的微分方程为：
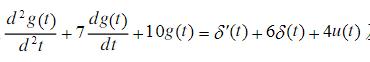用时域分析法求解系统的阶跃响应。
关注下方微信公众号，在线模考后查看
热门试题
- 一个离散LTI系统的网络函数H（z）的极
- 在如图所示的系统中，周期信号p（t）是一
- 如某连续因果系统的特征方程为D（s）=s
- 已知因果信号的拉普拉斯变换为（）
- 系统函数H（s）与激励信号E（s）成反比
- 设的收敛域为Re{s}＞-1，&ensp
- 用拉氏变换分析法，求系统的响应
- 一线性时不变离散时间因果系统的直接型模拟
- 试求图A-4所示信号的频谱F（j&ome
- 有限长序列f（n）=3δ（n）+2δ（n
- 如图所示，已知某连续系统，其中系统的单位
- 利用z平面零极点分布的几何作图法粗略画出
- 已知系统的差分方程、输入和初始状态如下，
- 连续周期信号f（t）的频谱F（jω）的特
- 图题所示反馈电路中，kv2
- 离散时间信号，则x（n）是（）
- 周期信号f（t）的双边频谱如图所示，写出
- 下列说法不正确的是（）
- 系统差分方程为y（n）=3y（n-1）+
- 已知变换 若收敛域|z|>2，则逆变换为