试题详情
- 简答题 如图所示为矩形截面水坝,其右侧受静水压力,顶部受集中力作用。试写出水坝的应力边界条件(下边界不写)。

-
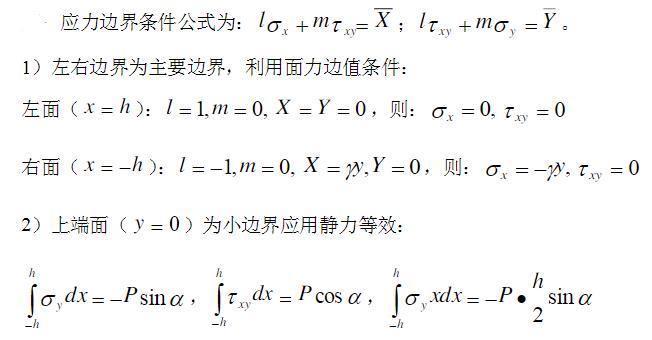
关注下方微信公众号,在线模考后查看

热门试题
- 在有限元分析计算中,为了保证解答的收敛性
- 关于弹性力学平面问题的极坐标解,下列说法
- 验证三角形单元的位移差值函数满足
- 用刚度集成法求下图所示结构的整体刚度矩阵
- 下列关于薄膜比拟方法的说法,有错误的是(
- 如下图所示三角形薄板,按三结点三角形单元
- 设有矩形截面的悬臂梁,在自由端受有集中荷
- 设有内半径为r。外半径为R的圆筒受内压力
- 弹性力学的基本假设是什么。
- 图示等腰直角三角形单元
- 下图所示的墙,高度为h,宽度为b,h?b
- 按应力求解平面问题时常采用位移法和应力法
- 每个单元的位移一般总是包含着两部分:一部
- 试简述力学中的圣维南原理,并说明它在弹性
- 一组可能的应力分量应满足:(),()。
- 简述有限元分析求得的位移解收敛于真实解得
- 已知平面应变状态下,变形体某点的位移函数
- 悬臂梁在自由端承受集中力F和弯矩M的作用
- 试导出极坐标和直角极坐中位移变量的坐标变
- 根据扭转应力函数在横截面边界为零的性质,