试题详情
简答题设有一个马尔可夫信源，它的状态集为{s1，s2，s3}，符号集为{a1，a2，a3}，及在某状态下发符号的概率为P（ak/si）（i，k=1，2，3），如图所示。 （1）求出图中马尔可夫信源的状态极限概率并找出符号的极限概率。 （2）计算信源处在某一状态下输出符号的条件熵H(X/S=j)(j=s1,s2,s3)。 （3）求出马尔可夫信源熵H。



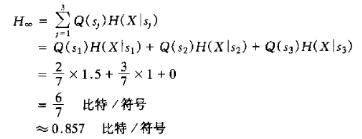
  • 关注下方微信公众号，在线模考后查看

热门试题