试题详情
- 简答题 设C是长度为n,最小距离为7的二元完备码。证明n=7或n=23。 证明:由完备码的定义可知,一个完备码必须满足下列条件:
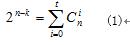
-

同理,可证得n=23时,同样满足(1)式。
故可证明当n=7或n=23时,C是二元完备码。 关注下方微信公众号,在线模考后查看

热门试题
- 信源编码
- 请给出域的定义并说明集合{0,1,2}可
- 考虑下图所示的二元信道,设发送二元符号的
- 信道无失真传递信息的条件是信息率小于信道
- 信息的基本概念在于它的()。
- 设离散无记忆信源,其发出的消息为(202
- 简述马尔可夫信源的定义及其极限熵。
- 信源的冗余度来自两个方面,一是信源符号之
- 黑白气象传真图的消息只有黑色和白色两种
- 若有两个串接的离散信道,它们的信道矩阵都
- 简述平均互信息量关于信源概率和信道转移概
- 给定语声样值X的概率密度为,求H
- 设有一离散信道,其信道传递矩阵为 并设
- 简述连续信道,连续信道的C的定义。
- 对于限平均功率的一维连续信源,当概率密度
- 试证明连续信源X的相对熵h(X)是概率密
- 在无失真的信源中,信源输出由()来度量;
- 设有一个信源,它产生0,1序列的信息。它
- 什么是香农容量公式?为保证足够大的信道容
- 一阶马尔可夫信源的状态图如图所示。信源X