试题详情
简答题 给定系统状态空间模型 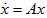（1）试问如何判断该系统在李雅普诺夫意义下的稳定性？ （2）试通过一个例子说明您给出的方法； （3）给出李雅普诺夫稳定性定理的物理解释。


  • （3）李雅普诺夫稳定性定理的物理意义：针对一个动态系统和确定的平衡状态，通过分析该系统运动过程中能量的变化来判断系统的稳定性。具体地说，就是构造一个反映系统运动过程中能量变化的虚拟能量函数，沿系统的运动轨迹，通过该能量函数关于时间导数的取值来判断系统能量在运动过程中是否减少，若该导数值都是小于零的，则表明系统能量随着时间的增长是减少的，直至消耗殆尽，表明在系统运动上，就是系统运动逐步趋向平缓，直至在平衡状态处稳定下来，这就是李雅普诺夫意义下的稳定性

  • 关注下方微信公众号，在线模考后查看

热门试题