试题详情
- 简答题 实际被控系统通常是连续时间系统，但计算机控制却是一种基于离散模型的控制，因此需要对连续时间系统做离散化。那么请问 （1）一个能控能观的连续时间系统，其离散化后的状态空间模型是否仍然保持能控能观性？ （2）以如下线性定常系统为例：
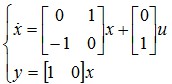显然它是状态完全能控且能观测的。并已知此系统的状态转移矩阵为 
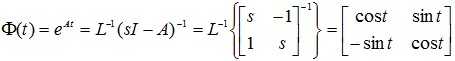确定使相应的离散化系统能控且能观测的采样周期的范围。并由此说明你所给出（1）的观点的理由。
-
关注下方微信公众号，在线模考后查看
热门试题
- 设某单位反馈系统的开环传递函数 要求闭环
- 求下列系统在单位阶跃输入时的输出y（t）
- 判断下列系统的能控性和能观测性并说明理由
- 反馈控制可改变系统的稳定性、动态性能，但
- 给定系统的状态空间表达式为 设计一个具
- 利用李亚普诺夫第一方法判定系统的稳定性。
- 判断下列二次型函数的符号性质：
- 已知受控系统传递函数为， 综合指标为：&
- 已知系统1、2的传递函数分别为求两系统串
- 已知某系统的方块图如下， 回答下列问题
- 设随动系统如图所示，图中K1<
- 某2阶非线性系统的状态方程为，证明该系统
- 控制系统如图所示。若要求校正后的静态速度
- 建立一个合理的系统模型是进行系统分析和设
- 试将下列系统按能控性和能观性进行结构分解
- 对一个由状态空间模型描述的系统，试回答
- 已知对象的状态空间模型，是完全能观的，请
- 若一个系统是李雅普诺夫意义下稳定的，则该
- （1）能够通过状态反馈实现任意极点配置的
- 下列矩阵是否满足状态转移矩阵的条件，如果