试题详情
简答题怎样判断迭代法收敛的快慢？一个迭代公式要达到P阶收敛需要什么条件？
  • 衡量迭代法快慢要看收敛阶P的大小，若序列（xk）收敛于x*，记为εk=xk-x*若存在P≥1及a>0，使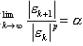，则称序列（xk）为P阶收敛，P越大收敛越快，当P＝1，则越小，收敛越快。一个迭代公式xk+1=φ（xk）若x*为φ的不动点，P为大于1的整数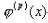，在x*连续，且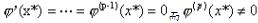，则此迭代公式为P阶收敛。

  • 关注下方微信公众号，在线模考后查看

热门试题