试题详情
- 简答题设地球的半径为R，质量是m′.证明人造卫星在地球引力场中以椭圆轨道运动的速率由下式表示：
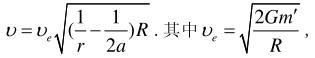是质点能脱离地球的逃逸速度，即第二宇宙速度；a是卫星轨道半长轴的长度.
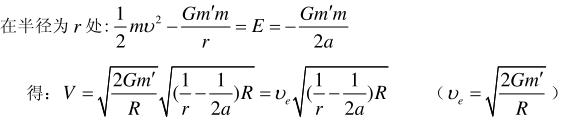
关注下方微信公众号，在线模考后查看
热门试题
- 杆系由球铰连接，位于正方体的边和对角线上
- 等边六角形连杆铅直放置，各杆间用光滑铰链
- 凸轮导板机构中，偏心轮的偏心距OA=e。
- 如图，轻质杠杆AB可绕O点转动，在A、B
- 均质圆柱重力P，半径为r，搁在不计自重的
- 平面机构如图所示。已知：OA=AB=20
- 图示空间构架由三根不计自重的有杆组成，在
- 曲柄肘杆压床机构已知：OA=0.15m，
- 在怎样的运动中，只有aτ
- 匀质圆盘的质量为m1
- 下列说法中正确的有（）。
- 两个半径相同，均质等厚的铁圆盘和木圆盘，
- 机构如右上图所示，O1
- 在地球表面以很大的速度v0
- 在一光滑水平直管中有一质量为m的小球，此
- 相互啮合的两个齿轮的传动比（）
- 设弹簧的原长为l0
- 根据空间任意力系的平衡方程至多可以解出（
- 已知刚体（动系）相对于定系的位置可用欧拉
- 某瞬时平面图形内任意两点A、B的速度分别