试题详情
简答题请结合你的工作或生活，谈谈对行动的可信性的理解，有什么方法可以建立可信的策略行动。
  • 每一种策略性行动都面临着可信性的问题，人们不一定相信策略性行动的提出者会实施其行动。因此提出者必须做一些辅助工作让人相信他会在第二阶段实施他已宣布的事。
    比如，工作中管理者对员工上班时间玩游戏的态度有所不同。一些管理者对员工很宽容，并不惩罚玩游戏的员工。另一些管理者则十分严厉，会处罚玩游戏的员工。一些管理者虽然说了会处罚的承诺，但禁不住员工的好话及其它员工的求情，就原谅了员工。从博弈论角度分析，假设三种管理者手下的员工各方面都相同，哪一种管理者将得到最高的支付呢？管理者对玩游戏的态度可以是“处罚”或“原谅”，员工可以“玩游戏”或“不玩游戏”，如下表所示：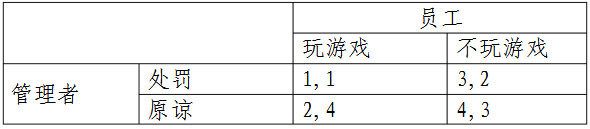
    管理者并不希望自己不近人情，故他们最好的结果就是(4,3)，最不好的结果就是(1,1);余下的两个策略，因管理者希望员工不玩游戏，故(3,2)好于(2,4)。员工最喜欢(4,3),最不好的结果也是(1,1)，余下的，员工(2,4)好于(3,2)。在此博弈中，若同时行动，或者是管理者后行动，与处罚带来的1和3的支付相比，原谅能带来2和4，是占优策略。此时，员工则会选择玩游戏。最终，均衡的结果是（2,4）。而如果管理者一开始就承诺“处罚”的话，员工会发现不玩游戏会更好，于是管理者得到了支付3。但是如果有员工曾被管理者原谅，可能他就会认为管理者心软，不相信管理者做出的“处罚”承诺，从而玩游戏。此时，就会得到一个最坏的结果，即（处罚，玩游戏），其支付仅为（1,1）。
    通过采取某种行动，改变博弈以得到更好的结果，这就是策略行动。策略行动分：承诺、威胁及许诺。这三种策略性行动最重要的，是必须让博弈的其他参与人相信策略性行动的提出者在第二阶段中确实会做其在第一阶段中宣布的事。而在此每一种策略行动都面临着可信性的问题，人们不一定相信策略行动的提出者会实施其行动。因此仅仅宣布是不够的。在第一阶段，提出者必须做一些辅助工作让人相信其会在第二阶段做已宣布的事。上述博弈中涉及的是管理者对玩游戏员工“处罚”态度的承诺。在这个事件中，管理者为了从策略行动中获得好处，他所做的承诺不能和同时行动博弈的均衡策略一样，因此管理者选择了“处罚”的承诺，这个策略行动改变了员工的期望和行动。一旦员工相信这种承诺，则他们会不玩游戏，从而得到（3，2）的支付。如果员工们尝试玩一次游戏，管理者可能会原谅他们，理由是“只此一次”，这里就存在了使策略性行动不付诸实践的诱惑， 使得承诺的可信性下降。如果最终员工不再相信“处罚”的承诺，则他们会玩游戏，从而最终管理者和员工只得到（1,1）的支付，双方利益均受损。这就是管理者铁石心肠的原因。因为他清楚破例原谅员工一次的危险性。因此，管理者需要做一些事情来确立他策略行动的可信性，即让其他参与人相信他们的行动如违背你的承诺，你将一定会付诸实践，而不会因人情等引诱而放弃。避免危险的办法通常只有一个，那就是绝不越雷池半步。并且管理者们需要找到某些方法使其的拒绝合理可信，同时提高其策略行动的可信性。第一、通过减少未来行动的自由，排除引诱行动，只能实施策略行动中所确定的行动。例如，管理者可以拿规章制度或工作纪律做挡箭牌，这些制度纪律一旦制定则个别管理者就不能在任何特殊情况下破例。这样做，就等于将“原谅”行动从他们的选择组合中剔除了，因此他只能实施“处罚”的承诺。规则的存在让员工相信管理者不可能再改变想法，所以此时管理者“处罚”的承诺就是可信的了。第二、改变未来的支付， 减少引诱行动的支付使实施策略行动成为最佳行动。管理者可以通过几次毫不让步的处罚建立起严厉的声誉，虽然毫不让步的处罚可能不是一件愉快的事，也可能违背管理者的本意，但这在漫长的工作生涯中是有好处的。因为如果一个管理者被认为非常严厉，就没有员工想用借口搪塞他，而他也就减少了拒绝员工的不愉快。如果管理者在一个博弈里未能兑现他的承诺，他的声誉将受到损害，这也就导致他在其他的博弈里得到低的支付。由此观之，提高策略行动的可信性将有助于提高策略性博弈中获得的支付。因此，学会运用坚守原则、提高声誉等方法增强自己行为的可信性，能帮助我们在今后的生活中选择最佳行为，获得更高的收益。

  • 关注下方微信公众号，在线模考后查看

热门试题