试题详情
简答题 双足直立机器人可以近似为一个倒立摆装置，如图所示。假设倒立摆系统的一个平衡点线性化状态空间模型如下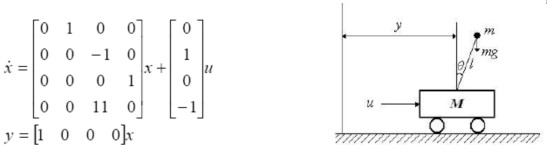： 其中，状态变量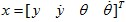，y是小车的位移，θ是摆杆的偏移角，u是作用在小车上的动力。试回答 （1）双足直立机器人在行走过程中被人推了一把而偏离垂直面，那么根据倒立摆原理，请问双足直立机器人在该扰动推力消失后还能回到垂直面位置吗？ （2）如果不能，那么请你从控制学的角度，给出两种能够使双足直立机器人在扰动推力消失后回到垂直面位置的方法。 （3）请结合倒立摆模型，简单叙述双足直立机器人能控性的含义。 （4）在状态反馈控制器设计中，需要用到系统的所有状态信息，但根据倒立摆原理，可测量的状态信息只有水平移动的位移y，那么你有什么方法可以实现这个状态反馈控制器的设计？你所用方法的条件是什么？依据是什么？请结合倒立摆模型，给出你使用方法的实现过程。
  • （1）不能，因为倒立摆是一个开环不稳定系统；
    （2）对于给定的倒立摆模型，是一线性时不变系统，因此可以用如下方法使双足直立机器人在扰动推力消失后回到垂直面位置（即稳定化控制器设计）：极点配置方法；基于李雅普诺夫稳定性理论的直接设计法；线性二次型最优控制器设计方法。
    （3）当双足直立机器人由于受初始扰动而稍稍偏离垂直面位置时，总可以通过对其施加一个适当的外力，使得将它推回到垂直面位置（将非零的初始状态转移到零状态）。
    （4）如果被控系统是状态能观的，那么通过设计（降维）状态观测器将不可测量状态变量观测输出，再应用线性定常系统的分离性原理，实现状态反馈控制器设计。结合倒立摆模型，则检验上述状态空间模型的能观性；系统完全能观，则对系统设计状态观测器（或对不可测量子系统和设计降维状态观测器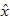）；应用线性定常系统的分离性原理，将状态反馈控制器u=-Kx中的状态x替换为观测状态从实现基于状态观测器的状态反馈控制器设计。
    使用方法的条件是：系统完全能观或不可观子系统是渐进稳定的；
    使用方法的依据是：线性定常系统的分离性原理。

  • 关注下方微信公众号，在线模考后查看

热门试题