试题详情
- 简答题第一次数学危机,是数学史上的一次重要事件,发生于大约公元前400年左右的古希腊时期,自()的发现起,到公元前370年左右,以()的定义出现为结束标志。这次危机的出现冲击了一直以来在西方数学界占据主导地位的毕达哥拉斯学派。
-
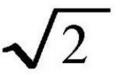 ;无理数
;无理数
关注下方微信公众号,在线模考后查看

热门试题
- 哥德尔不完全性定理一举粉碎了数学家两千年
- 论述数学的三次危机对数学发展的作用。
- 人们运用类比法,根据一类事物所具有的某种
- 第二次数学危机,指发生在十七、十八世纪,
- 例如,“等腰直角三角形→等腰三角形→直角
- 在反例反驳中,构造一个反例必须满足条件:
- 如果某一问题存在算法,并进一步构造出这个
- 数学分类有现象分类和本质分类的区别。所谓
- 学科课程是整个教学过程中的主渠道,当然成
- 圆周角定理证明思路如下:将圆周角的两边所
- 英国的牛顿和德国的莱布尼兹分别以()为背
- 鸽笼原理可叙述为:若n+1只鸽子飞进n个
- 叙述概括的含义及其过程。
- 古希腊欧几里得的《几何原本》是人们所建立
- 简述数学建模的基本步骤。
- 《九章算术》的叙述方式以()为主,先给出
- 所谓本质分类,即根据事物的()进行分类。
- 古印度人对时间和空间的看法与现代天文学十
- 抽象是对同类事物抽取其()的本质属性或特
- 在丢番图时代(约250)以前的一切代数学