试题详情
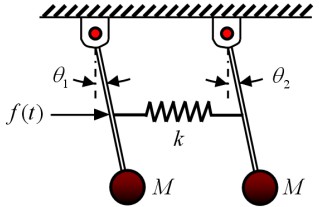
简答题 如图所示为一个摆杆系统，两摆杆长度均为L，摆杆的质量忽略不计，摆杆末端两个质量块（质量均为M）视为质点，两摆杆中点处连接一条弹簧，θ1与θ2分别为两摆杆与竖直方向的夹角。当θ1=θ2时，弹簧没有伸长和压缩。水平向右的外力f（t）作用在左杆中点处，假设摆杆与支点之间没有摩擦与阻尼，而且位移足够小，满足近似式sinθ=θ，cosθ=1。 （1）写出系统的运动微分方程； （2）写出系统的状态方程。

  • 关注下方微信公众号，在线模考后查看

热门试题