试题详情
- 简答题 设有方程组Ax=b,其中A为对称正定阵,迭代公式
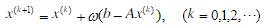 试证明当0<ω<2/β时上述迭代法收敛(其中0<α≤λ(A)≤β)。
试证明当0<ω<2/β时上述迭代法收敛(其中0<α≤λ(A)≤β)。
-
所给迭代公式的迭代矩阵为B=I-ωA,
其n个特征值分别为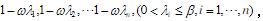 ,
当0<ω<2/β时,有-1<1-ωλi<1,(i=1,2,...,n)
,
当0<ω<2/β时,有-1<1-ωλi<1,(i=1,2,...,n)
因而ρ(B)<1,迭代法收敛。 关注下方微信公众号,在线模考后查看

热门试题
- 证明
- 用列主元消去法解线性方程组
- 设f(x)=C2[
- 设xj为互异节点(
- 等距二点求导公式f′(x1)≈()
- 用劈因子法解方程x3
- 用适当的迭代法求下列方程组的根,精确至4
- 矩阵第一行乘以一数,成为 证明当时,c
- 令Tn(x)=T<
- 设A∈Rn×n,求
- 为求方程x3-x<
- 由下列数表进行Newton插值,所确定的
- 应用牛顿法于方程,导出求的迭代公式,并用
- 试用复化梯开公式计算曲线f(x)=tan
- 如何选取r,使p(x)=x2<
- 用Romberg方法求,要求误差不超过。
- f(1)=-1,f(2)=2,f(3)=
- 研究求的牛顿公式 证明对一切k=1.2
- 将矩阵A分解为单位下三角矩阵L和上三角矩
- 试用消元法解方程组假定只用三位数计算,问